Классификация сейсмических сигналов на основе нейросетевых технологийАннотация В данном дипломе рассматривается задача классификации сейсмических сигналов по типу источника, т.е. определение по записанной сейсмограмме землетрясений или взрывов. Основная цель диплома состоит в исследовании возможности применения аппарата нейронных сетей для решения поставленной задачи и сравнение эффективности такого решения со стандартными аналитическими методами. Оглавление Аннотация Введение 1. Основные положения теории нейронных сетей 2. Постановка задачи классификации сейсмических сигналов 3. Статистическая методика решения задачи классификации 3.1. Выделение информационных признаков из сейсмограмм 3.2. Отбор наиболее информативных признаков для идентификации 3.3. Процедуры статистической идентификации 3.4. Оценка вероятности ошибочной классификации методом скользящего экзамена 4. Обзор различных архитектур нейронных сетей, предназначенных для задач классификации 4.1. Нейрон-классификатор 4.2. Многослойный персептрон 4.3. Сети Ворда 4.4. Сети Кохонена 4.5. Выводы по разделу 5. Методы предварительной обработки данных 5.1. Максимизация энтропии как цель предобработки 5.2. Нормировка данных 5.3. Понижение размерности входных данных 5.3.1. Отбор наиболее информативных признаков 5.3.2. Сжатие информации. Анализ главных компонент 5.4. Выводы по разделу 6. Реализация нейросетевой модели и исследование ее технических характеристик 6.1. Структура нейросети 6.2. Исходные данные 6.3. Определение критерия качества системы и функционала его оптимизации 6.4. Выбор начальных весовых коэффициентов 6.5. Алгоритм обучения и методы его оптимизации 6.6. Формирование обучающей выборки и оценка эффективности обученной нейросетевой модели 7. Программная реализация 7.1. Функциональные возможности программы 7.2. Общие сведения 7.3. Описание входного файла с исходными данными 7.4. Описание файла настроек 7.5. Алгоритм работы программы 7.6. Эксплуатация программного продукта 7.7. Результат работы программы 8. Заключение Список литературы Приложение
Введение Применение аппарата нейронных сетей для решения различных задач науки и техники обусловлено огромными потенциальными возможностями, этих технологий. Существуют задачи, решение которых просто невозможно аналитическими методами, а нейросети успешно с ними справляются. Даже в том случае, если можно найти решение при помощи уже изученных алгоритмов, нейронные сети порой позволяют сделать то же самое быстрее и более эффективно. В данном дипломе рассматривается задача, возникающая при сейсмическом мониторинге, — классификация сейсмических сигналов по типу источника, т.е. определение по записанной сейсмограмме землетрясений или взрывов. Несмотря на то, что для ее решения, в настоящее время успешно применяются методы статистического анализа, продолжается поиск более эффективных алгоритмов, которые бы позволили проводить классификацию точнее и с меньшими затратами. В качестве таких методов предлагается использовать аппарат нейронных сетей. Основная цель дипломной работы — исследовать возможность применения нейронных сетей для идентификации типа сейсмического сигнала, выяснить, насколько данное решение будет эффективным в сравнении с уже используемыми методами. Первая глава посвящена описанию основных положений теории нейронных сетей, а также областям науки и техники, в которых эти технологии нашли широкое применение. Последующие два раздела предназначены формализовать на математическом уровне задачу классификации сейсмических сигналов и способе ее решения на основе статистических методов. Обзор различных архитектур нейронных сетей, предназначенных для решения задачи классификации, их основные положения, достоинства и недостатки, а также методы предварительной подготовки данных приведены в разделах 4 и 5. В шестом разделе говорится непосредственно о нейросетевом решении рассматриваемой задачи, построенном на основе известной и часто используемой парадигмы — многослойного персептрона, детально обсуждаются основные алгоритмы обучения, выбора начальных весовых коэффициентов и методы оценки эффективности выбранной модели нейронной сети. В разделе “Программная реализация” описывается специально разработанная программа, реализующая основные идеи нейросетевого программирования и адаптированная для решения поставленной задачи. Также в этом разделе представлены результаты экспериментов по обработке сейсмических сигналов, проведенных на базе созданной программы. В заключении изложены основные выводы и рекомендации по направлению дальнейших исследований в применении нейронных сетей для решения задачи классификации сейсмических сигналов. 1. Основные положения теории нейронных сетей Для того, чтобы обсуждать возможности нейросетевых технологий, необходимо хотя бы немного иметь представление об элементарных понятиях, о том, что же такое нейрон, нейронная сеть, из чего она состоит и какие процессы в ней происходят. В нейроинформатике для описания алгоритмов и устройств выработана специальная “схемотехника” , в которой элементарные устройства — сумматоры, синапсы, нейроны и т.п. объединяются в сети, предназначенные для решения задач. Это своего рода особенный язык для представления нейронных сетей и их обсуждения. При программной и аппаратной реализации на этом языке описания переводятся на языки другого уровня, более пригодные для реализации. Элементы нейронных сетей Самыми простыми, базовыми элементами нейросетей являются:
Математическая модель нейрона:
w i — вес синапса (weight) , ( i=0,1,2... p ) ; w 0 — значение смещения (bias) ; s — результат суммирования (sum) ; x i — компонента входного вектора (входной сигнал) , ( i=1,2,... p ) ; y — выходной сигнал нейрона; p- число входов нейрона; f — нелинейное преобразование (функция активации) . В общем случае входной сигнал, весовые коэффициенты и значения смещения могут принимать действительные значения. Выход ( y ) определяется видом функции активации и может быть как действительным, так и целым. Во многих практических задачах входы, веса и смещения могут принимать лишь некоторые фиксированные значения. Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами — тормозящими. Таким образом, нейрон полностью описывается своими весами w i и передаточной функцией f(x) . Получив набор чисел (вектор) x k в качестве входов, нейрон выдает некоторое число y на выходе.
Эта модель была предложена Маккалоком и Питтсом еще в 1943 г. При этом использовались пороговые передаточные функции (рис. 2a) , и правила формирования выходного сигнала
y
выглядели особенно просто:
Нейронная сеть Нейронная сеть — это набор нейронов, определенным образом связанных между собой. Как правило, передаточные функции всех нейронов в сети фиксированы, а веса являются параметрами сети и могут изменяться. Одними из наиболее распространенных являются многослойные сети, в которых нейроны объединены в слои. Слой — это совокупность нейронов c единым входным сигналом. В качестве основного примера рассмотрим сеть, которая достаточно проста по структуре и в то же время широко используется для решения прикладных задач — двухслойный персептрон с p входами и одним выходом (рис. 1.3) . Как следует из названия, эта сеть состоит из двух слоев. Собственно нейроны располагаются в первом (скрытом) и во втором (выходном) слое. Входной слой (также его называют нулевым или “вырожденным” ) только передает входные сигналы ко всем H нейронам первого слоя (здесь H = 4 ) . Каждый нейрон первого слоя имеет p входов, которым приписаны веса w i0 , w i1 , w i2 ,..., w ip (для нейрона с номером i ) . Веса w i0 и v 0 соответствуют смещению b в описании формального нейрона, которое приведено выше. Получив входные сигналы, нейрон суммирует их с соответствующими весами, затем применяет к этой сумме передаточную функцию и пересылает результат на один из входов нейрона второго (“выходного” ) слоя. В свою очередь, нейрон выходного слоя суммирует полученные от первого слоя сигналы с некоторыми весами v i . Итак, подавая на входы персептрона любые числа x 1 , x 2 ,..., x p , мы получим на выходе значение некоторой функции F(x 1 , x 2 ,..., x p ) , которое является ответом (реакцией) сети. Очевидно, что ответ сети зависит как от входного сигнала, так и от значений ее весовых коэффициентов.
Выпишем точный вид этой функции
Разобравшись с тем, из чего состоят нейронные сети, и как они функционируют, перейдем к вопросу "как создать сеть, адаптированную для решения поставленной задачи? ". Этот вопрос решается в два этапа: (рис. 1.4)
На первом этапе следует выбрать следующее:
Эта задача на первый взгляд кажется необозримой, но, к счастью, необязательно придумывать нейросеть "с нуля" — существует несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные архитектуры — это многослойный персептрон, нейросеть с общей регрессией, сети Кохонена и другие. На втором этапе следует "обучить" выбранную сеть, то есть подобрать такие значения ее весов, чтобы сеть работала нужным образом. Необученная сеть подобна ребенку — ее можно научить чему угодно. В используемых на практике нейросетях количество весов может составлять несколько десятков тысяч, поэтому обучение — действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса сети определенным образом. Обучение нейросети Обучить нейросеть — значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы "А", мы спрашиваем его: "Какая это буква? " Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: "Это буква А". Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют "обучение с учителем". При обучении сети мы действуем совершенно аналогично. Пусть у нас имеется некоторая база данных, содержащая примеры из разных классов, которые необходимо научиться распознавать (набор рукописных изображений букв) . Предъявляя изображение буквы "А" на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ — в данном случае нам хотелось бы, чтобы на выходе с меткой "А" уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1,0,0,...) , где 1 стоит на выходе с меткой "А", а 0 — на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа — вектор ошибки. Далее применяя различные алгоритмы по вектору ошибки вычисляем требуемые поправки для весов сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте — тренировку. Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "сеть выучила все примеры", "сеть обучена", или "сеть натренирована". В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную сеть считают натренированной и готовой к применению на новых данных. Схематично процесс обучения представлен на рис 1.5. Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать сеть для распознавания буквы “A” , если в обучающей выборке она не была представлена. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров. Повторим еще раз, что обучение сети — сложный и наукоемкий процесс. Алгоритмы обучения имеют различные параметры и настройки, для управления которыми требуется понимание их влияния. Применение нейросети После того, как сеть обучена, ее можно применять для решения поставленной задачи (рис 1.4) . Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, можно читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейросеть, грамотным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, мы можем нарисовать букву "А" другим почерком, а затем предложить нашей сети классифицировать новое изображение. Веса обученной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения Примеры практического применения нейронных сетей. В качестве примеров рассмотрим наиболее известные классы задач, для решения которых в настоящее время широко применяются нейросетевые технологии. Прогнозирование Прогноз будущих значений переменной, зависящей от времени, на основе предыдущих значений ее и/или других переменных. В финансовой области, это, например, прогнозирование курса акций на 1 день вперед, или прогнозирование изменения курса валют на определенный период времени и т.д. (рис 1.6) . Распознавание или классификация Определение, к какому из заранее известных классов принадлежит тестируемый объект. Следует отметить, что задачи классификации очень плохо алгоритмизируются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейросеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос. Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес и т.д.) . Конечно, "мнение" сети в этом случае нельзя считать окончательным. Классификация предприятий по степени их перспективности (рис 1.8) — это уже привычный способ использования нейросетей в практике крупных компаний. При этом сеть также использует множество экономических показателей, сложным образом связанных между собой. Кластеризацию и поиск закономерностей Помимо задач классификации, нейросети широко используются для поиска зависимостей в данных и кластеризации. Например, нейросеть на основе методики МГУА (метод группового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде полинома (рис. 1.9) . Такая сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых) , которые не обнаруживаются стандартными статистическими методами. Кластеризация — это разбиение набора примеров на несколько компактных областей (кластеров) , причем число кластеров заранее неизвестно (рис. 1.10) . Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно быстро выявить фальсифицированные страховые случаи или недобросовестные предприятия. Несмотря на большие возможности, существует ряд недостатков, которые все же ограничивают применение нейросетевых технологий. Во-первых, нейронные сети позволяют найти только субоптимальное решение, и соответственно они неприменимы для задач, в которых требуется высокая точность. Функционируя по принципу черного ящика, они также неприменимы в случае, когда необходимо объяснить причину принятия решения. Обученная нейросеть выдает ответ за доли секунд, однако относительно высокая вычислительная стоимость процесса обучения как по времени, так и по объему занимаемой памяти также существенно ограничивает возможности их использования. И все же класс задач, для решения которых эти ограничения не критичны, достаточно широк. 2. Постановка задачи классификации сейсмических сигналов Международная система мониторинга (МСМ) , сформировавшаяся в мире за последние десятилетия, предназначена для наблюдения за сейсмически активными регионами. Основная часть информации фиксируется на одиночных сейсмических станциях. Дальнейшая обработка этой информации позволяет оценить различные физические параметры, характеризующие записанное событие. Соответственно чем информативнее записанный сигнал, тем больше всевозможных параметров можно определить и точнее. Относительно недавно для наблюдения стали использовать группы сейсмических станций. Наиболее широкое применение получили малоапертурные группы с диаметром приблизительно 3 км за счет того, что в этом случае можно пренебречь искажениями сигнала, возникающими из-за неоднородности земной поверхности. Причина использования сейсмических групп также заключается в том, что при таком методе наблюдения можно применять специальные алгоритмы комплексной обработки регистрируемой многоканальной сейсмограммы, которые обеспечивают лучшее качество оценки параметров записанной информации, в сравнении с одиночными сейсмическими станциями. Одна из многочисленных задач, возникающих при региональном мониторинге, это задача идентификации типа сейсмического источника или задача классификации сейсмических сигналов . Она состоит в том, чтобы по сейсмограмме определить причину возникновения зафиксированного события, т.е. различить взрыв и землетрясение. Ее решение предусматривает разработку определенного метода (решающего правила) , который с определенной вероятностью мог бы отнести записанное событие к одному из двух классов. На рис. 2.1 представлена схема постановки задачи. Для решения этой задачи в настоящее время применяются различные аналитические методы из теории статистического анализа, позволяющие с высокой вероятностью правильно классифицировать данные. Как правило, для конкретного региона существует своя база данных записанных событий. Она включает в себя пример сейсмограмм характеризующих как землетрясения, так и взрывы произошедшие в этом регионе с момента начала наблюдения. Все существующие методы идентификации используют эту базу данных в качестве обучающего множества, тем самым, улавливая тонкие различия характерные для данного региона, методы, настраивают определенным образом свои параметры и в итоге учатся классифицировать все обучающее множество на принадлежность к одному из двух классов. Один из наиболее точных методов основан на выделении дискриминантных признаков из сейсмограмм и последующей классификации векторов признаков с помощью статистических решающих правил. Размерность таких векторов соответствует количеству признаков, используемых для идентификации и, как правило, не превышает нескольких десятков. Математическая постановка в этом случае формулируется как задача разделения по обучающей выборке двух классов и ставится так: имеется два набора векторов (каждый вектор размерности N) : X 1 , …, X p1 и Y 1 , …Y p2 . Заранее известно, что X i (i=1, …, p1) относится к первому классу, а Y j (j=1, …, p2) — ко второму. Требуется построить решающее правило, т.е. определить такую функцию f, что при f(x) > 0 вектор x относился бы к первому классу, а при f(x) < 0 — ко второму, где xН {X 1 , …, X p1 , Y 1 , …, Y p2 }.
3. Статистическая методика решения задачи классификации В данном разделе рассматривается методика определения типов сейсмических событий, основанная на выделении дискриминантных признаков из сейсмограмм и последующей классификации векторов признаков с помощью статистических решающих правил. [8] 3.1 Выделение информационных признаков из сейсмограмм Исходные данные представлены в виде сейсмограмм (рис. 3.1) — это временное отображение колебаний земной поверхности. В таком виде анализировать информацию, оценивать различные физические характеристики зафиксированного события достаточно трудно. Существуют различные методы, специально предназначенные для обработки сигналов, которые позволяют выделять определенные признаки, и, в дальнейшем, по ним производить анализ записанного события. Как правило, в большинстве из этих методов на начальном этапе выполняется следующий набор операций:
а) Быстрое (дискретное) преобразование Фурье (БПФ) ; б) Затем накладываются характеристики определенного фильтра, например, фильтра Гаусса. в) Обратное преобразование Фурье (ОБПФ) , для того чтобы получить отфильтрованный сигнал. Далее применяются различные алгоритмы для формирования определенного признака. В частности, можно легко найти максимальную амплитуду колебания сигнала, характеристику определяемую выражением max{peakMax — peakMin }. Определив данный параметр для частоты f 1 допустим для P волны, а также для частоты f 2 для S волны можно найти их отношение P( f 1 ) /S( f 2 ) , и использовать его в качестве дискриминационного признака. Применяя другие алгоритмы, можно построить большое количество таких признаков. Однако, для задачи идентификации типа сейсмического события, важными являются далеко не все. Из наиболее информативных можно выделить такие признаки, как отношение амплитуд S и P волн, или доля мощности S фазы на высоких (низких) частотах по отношению к мощности S фазы во всей полосе частот. Как правило, максимальное количество признаков, которое используется для этой задачи составляет около 25 — 30. 3.2 Отбор наиболее информативных признаков для идентификации Как было показано выше, в сейсмограмме анализируемого события можно выделить достаточно много различных характеристик, однако, далеко не все из них могут действительно нести информацию, существенную для надежной идентификации взрывов и землетрясений. Многочисленные исследования в дискримининтном анализе показали, что выделение малого числа наиболее информативных признаков исключительно важно для эффективной классификации. Несколько тщательно отобранных признаков могут обеспечить вероятность ошибочной классификации существенно меньшую, чем при использовании полного набора. Ниже представлена процедура отбора наиболее информативных дискриминантных признаков, осуществляемая на основании обучающих реализаций землетрясений и взрывов из данного региона. [8] В начале каждый вектор x sj = (x (i) sj , iО 1, p) ; где sО 1,2 - номер класса ( s=1 — землетрясения s=2 — взрывы) , jО 1, n s , n s -число обучающих векторов данного класса состоит из p признаков, выбранных из эвристических соображений как предположительно полезные для данной проблемы распознавания. При этом число p может быть достаточно велико и даже превышать число имеющихся обучающих векторов в каждом из классов, но для устойчивости вычислений должно выполняться условие p < n 1 +n 2 . Процедура отбора признаков — итерационная и состоит из p шагов на каждом из которых число отобранных признаков увеличивается на единицу. На каждом промежуточном k -м шаге процедура работает с n1+n2 k -мерными векторами x sj (k) ( kЈ p) , сформированных из k-1 признаков, отобранных в результате первых k-1 шагов и некоторого нового признака из числа оставшихся. Отбор признаков основан на оценивании по векторам, состоящим из различных признаков, стохастического расстояния Кульбака-Махаланобиса D(k) между распределениями вероятностей векторов x sj (k) : D(k) = ( m (k, 1) — m (k, 2) ) T S -1 n1+n2 (k) ( m (k, 1) — m (k, 2) ) , (6) где: m (k, 1) , m (k, 2) k — мерные векторы выборочных средних, вычисленные по k -мерным векторам x 1j (k) jО 1, n 1 и x 2j (k) jО 1, n 2 первого и второго классов; S -1 n1+n2 (k) есть (kґ k) - мерная обратная выборочная матрица ковариаций, вычисленная с использованием всего набора k — мерных векторов x 1j (k) jО 1, n 1 и x 2j (k) jО 1, n 2 На первом шаге процедуры отбора значения функционала D(1) вычисляются для каждого из p признаков. Максимум из этих p значений достигается на каком то из признаков, который таким образом отбирается как первый информативный. На втором шаге значения функционала D(2) вычисляются уже для векторов, состоящих из пар признаков. Первый элемент в каждой паре — это признак, отобранный на предыдущем шаге, второй элемент пары — один их оставшихся признаков. Таким образом получаются p-1 значения функционала D(2) . Второй информативный признак отбирается из условия, что на нем достигается максимум функционала D(2) . Далее процедура продолжается аналогично, и на k -м шаге процедуры отбора вычисляются значения функционала D(k) по обучающим векторам, состоящим из k признаков. Первые k-1 компонент этих векторов есть информативные признаки, отобранные на предыдущих k-1 шагах, последняя компонента — один из оставшихся признаков. В качестве k -го информативного признака отбирается тот признак, для которого функционал D(k) -максимален. Описанная процедура ранжирует порядок следования признаков в обучающих векторах так, чтобы обеспечить максимально возможную скорость возрастания расстояния Махаланобиса (6) с ростом номера признака. Для селекции множества наиболее информативных признаков на каждом шаге k=1,2,..., p описанной выше итерационной процедуры ранжирования признаков по информативности сохраняются номер j(k) в исходной таблице признаков и имя выбранного признака, также вычисляется теоретическое значение полной вероятности ошибки классификации P(k) по формуле Колмогорова-Деева [12]. P(k) = (1/2) [1 — T k (D(k) /s (k) ) + T k (-D(k) / s (k) ) ], где k — число используемых признаков s 2 (k) = [(t+1) /t][r 1 +r 2 +D(k) ]; t = [(r 1 +r 2 ) /r 1 r 2 ]-1; r 1 =k/n 1 ; r 2 =k/n 2 (7) T k (z) = F(z) + (1/(k-1) ) (a 1 — a 2 H 1 (z) + a 3 H 2 (z) — a 4 H 3 (z) ) f(z) , F(z) — функция стандартного Гауссовского распределения вероятностей; f(z) — плотность этого распределения; H i (z) — полином Эрмита степени i , i=1,2,3; a j , j=1,..., 4 — некоторые коэффициенты, зависящие от k, n 1 , n 2 и D(k) [12]. Эта формула, как было показано в различных исследованиях, имеет хорошую точность при размерах выборок порядка сотни и r s <0.3, s=1,2. Функция D(k) , получаемая в результате процедуры ранжирования признаков, возрастает с ростом k , однако, на практике ее рост, как правило, существенно замедляется при k® p. В этом случае функция P(k) на каком то шаге k 0 между 1 и p имеет минимум. В качестве набора наиболее информативных признаков и принимается совокупность признаков, отобранных на шагах 1 ,..., k 0 описанной выше процедуры. Именно они обеспечивают минимальную полную вероятность ошибочной классификации, которая может быть получена при данных обучающих наблюдениях. 3.3 Процедура статистической идентификации. В качестве решающего правила используются алгоритмы идентификации, основанные на классических статистических дискриминаторах, таких как линейный и квадратичный дискриминаторы. Данные алгоритмы применяются наиболее часто в виду простоты их использования, удобства обучения применительно к конкретному региону и легкости оценивания вероятности ошибочной идентификации взрывов и землетрясений для каждого конкретного региона. Их роль как эффективных правил выбора решения при идентификации особенно возрастает, если применять эти алгоритмы к множествам обучающих и идентифицируемых векторов, составленных из наиболее информативных для данного региона дискриминантных признаков, отобранных в соответствии с описанной выше методикой.
Линейная дискриминантная функция описывается следующей формулой:
Квадратичная дискриминационная функция описывается следующей формулой
3.4 Оценка вероятности ошибочной классификации методом скользящего экзамена Оценивание вероятности ошибочной идентификации типа событий (землетрясение-взрыв) , в каждом конкретном регионе представляет собой одну из основных практических задач мониторинга. Эту задачу приходится решать на основании накопления региональных сейсмограмм событий, о которых доподлинно известно, что они порождены землетрясениями или взрывами. Эти же сейсмограммы представляют собой "обучающие данные" для адаптации решающих правил. Из теории распознавания образов известно, что наиболее точной и универсальной оценкой вероятности ошибок классификации является оценка, обеспечиваемая процедурой “скользящего экзамена” (“cross-validation” ) [11]. В методе скользящего экзамена на каждом шаге один из обучающих векторов x sj , jО 1, n s , sО 1,2, исключается из обучающей выборки. Оставшиеся векторы используются для адаптации (обучения) LDF или QDF или любого другого дискриминатора. Исключенный вектор затем классифицируется с помощью дискриминатора, обученного без его участия. Если этот вектор классифицируется неправильно, т.е. относится к классу 2 вместо класса 1 или наоборот, соответствующие “счетчики” n 12 или n 21 увеличиваются на 1. Исключенный вектор затем возвращается в обучающую выборку, а изымается уже другой вектор x s(j+1) . Процедура повторяется для всех n l + n 2 обучающих векторов. Вычисляемая в результате величина p 0 =(n 12 +n 21 ) /(n l +n 2 ) является состоятельной оценкой полной вероятности ошибочной классификации. Значения дискриминатора, полученные в результате процедуры скользящего экзамена для обоих классов, ранжируются по амплитуде: ранжированные последовательности удобнее сравнивать с порогом и делать выводы о “физических” причинах ошибочной классификации. 4. Обзор различных архитектур нейронных сетей, предназначенных для задач классификации Приступая к разработке нейросетевого решения, как правило, сталкиваешься с проблемой выбора оптимальной архитектуры нейронной сети. Так как области применения наиболее известных парадигм пересекаются, то для решения конкретной задачи можно использовать совершенно различные типы нейронных сетей, и при этом результаты могут оказаться одинаковыми. Будет ли та или иная сеть лучше и практичнее, зависит в большинстве случаев от условий задачи. Так что для выбора лучшей приходится проводить многочисленные детальные исследования. Рассмотрим ряд основных парадигм нейронных сетей, успешно применяемых для решения задачи классификации, одна из постановок которой представлена в данной дипломной работе. 4.1 Нейрон — классификатор
Простейшим устройством распознавания образов в нейроинформатике является одиночный нейрон (рис. 4.1) , превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных [1-5,7,10]:
Итак, в p-мерном пространстве задана обучающая выборка x 1 , …, x n (первый класс) и y 1 , …, y m (второй класс) . Требуется найти такие p+1- мерный вектор w , что для всех i=1, …, n и j=1, …, m w 0 +(x i , w) >0 и w 0 +(y j , w) <0. Переформулируем задачу, сведя ее к отделению нуля от конечного множества векторов в p+1 — мерном пространстве. Для этого рассмотрим p+1 — мерные векторы z l (l=0,1, …., n+m) :
Когда за весь цикл нет ни одной ошибки (т.е. модификации w ) , то решение w найдено, в случае же ошибок полагаем l=1 и снова проходим цикл. В некоторых простейших случаях линейный дискриминатор — наилучший из возможных, а именно когда оба класса можно точно разделить одной гиперплоскостью, рисунок 4.2 демонстрирует эту ситуацию для плоскости, когда p=2 .
4.2 Многослойный персептрон Возможности линейного дискриминатора весьма ограничены. Для решения более сложных классификационных задач необходимо усложнить сеть вводя дополнительные (скрытые) слои нейронов, производящих промежуточную предобработку входных данных, таким образом, чтобы выходной нейрон-классификатор получал на свои входы уже линейно-разделимые множества. Такие структуры носят название многослойные персептроны [1-4,7,10] (рис. 1.3) . Легко показать, что, в принципе, всегда можно обойтись одним скрытым слоем, содержащим, достаточно большое число нейронов. Действительно, увеличение скрытого слоя повышает размерность пространства, в котором выходной нейрон производит классификацию, что, соответственно, облегчает его задачу. Персептроны весьма популярны в нейроинформатике. И это обусловлено, в первую очередь, широким кругом доступных им задач, в том числе и задач классификации, распознавания образов, фильтрации шумов, предсказание временных рядов, и т.д., причем применение именно этой архитектуры в ряде случаев вполне оправдано, с точки зрения эффективности решения задачи. Рассмотрим какие алгоритмы обучения многослойных сетей разработаны и применяются в настоящее время. [7,10]. В основном все алгоритмы можно разбить на две категории:
К первой группе относятся те, которые основаны на вычислении производной функции ошибки и корректировке весов в соответствии со значением найденной производной. Каждый дальнейший шаг направлен в сторону антиградиента функции ошибки. Основу всех этих алгоритмов составляет хорошо известный алгоритм обратного распространения ошибки (back propagation error) . [1-5,7,10].
3. RPROP (от resilient –эластичный) , в котором каждый вес имеет свой адаптивно настраиваемый темп обучения. [4] 4. Методы второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных. [3,4,7]. Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям характеристик сети. К этой группе алгоритмов относятся такие как:
Основным недостатком этой группы алгоритмов является очень долгое время обучения, а соответственно и большие вычислительные затраты. Однако, как пишут в различных источниках, эти алгоритмы обеспечивают глобальную оптимизацию, в то время как градиентные методы в большинстве случаев позволяют найти только локальные минимумы функционала ошибки. Известны также алгоритмы, которые основаны на совместном использовании обратного распространения и обучения Коши. Коррекция весов в таком комбинированном алгоритме состоит из двух компонент: направленной компоненты, вычисляемой с использованием алгоритма обратного распространения, и случайной компоненты, определяемой распределением Коши. Однако, несмотря на хорошие результаты, эти методы еще плохо исследованы. 4.3 Сети Ворда Одним из вариантов многослойного персептрона являются нейронные сети Ворда. Они способны выделять различные свойства в данных, благодаря наличию в скрытом слое нескольких блоков, каждый из которых имеет свою передаточную функцию (рис. 4.4) . Передаточные функции (обычно сигмоидного типа) служат для преобразования внутренней активности нейрона. Когда в разных блоках скрытого слоя используются разные передаточные функции, нейросеть оказывается способной выявлять новые свойства в предъявляемом образе. Для настройки весовых коэффициентов используются те же алгоритмы, о которых говорилось в предыдущем разделе.
4.4. Сети Кохонена Сети Кохонена — это одна из разновидностей нейронных сетей, для настройки которой используется алгоритм обучения без учителя. Задачей нейросети Кохонена является построение отображения набора входных векторов высокой размерности на карту кластеров меньшей размерности, причем таким образом, что близким кластерам на карте отвечают близкие друг к другу входные векторы в исходном пространстве. Сеть состоит из M нейронов, образующих, как правило одномерную или двумерную карту (рис. 4.2) . Элементы входных сигналов {x i } подаются на входы всех нейронов сети. В процессе функционирования (самоорганизации) на выходе слоя Кохонена формируются кластеры (группа активных нейронов определённой размерности, выход которых отличен от нуля) , характеризующие определённые категории входных векторов (группы входных векторов, соответствующие одной входной ситуации) . [9] Алгоритм Кохонена формирования карт признаков. Шаг 1. Инициализировать веса случайными значениями. Задать размер окрестности s (0) , и скорость h (0) и t max . Шаг 2. Задать значения входных сигналов (x 1 , …, x p ) .
Шаг 3.
Вычислить расстояние до всех нейронов сети. Расстояния d
k
от входного сигнала
x
до каждого нейрона
k
определяется по формуле:
Шаг 4. Найти нейрон — победитель, т.е. найти нейрон j, для которого расстояние d j наименьшее: j: d j < d k " k№ p Шаг 5 . Подстроить веса победителей и его соседей.
Благодаря своим способностям к обобщению информации, карты Кохонена являются удобным инструментом для наглядного представления о структуре данных в многомерном входном пространстве, геометрию которого представить практически невозможно. Сети встречного распространения. Еще одна группа технических применений связана с предобработкой данных. Карта Кохонена группирует близкие входные сигналы Х, а требуемая функция Y = G(X) строится на основе обычной нейросети прямого распространения (например многослойного персептрона или линейной звезды Гроссберга[1]) к выходам нейронов Кохонена. Такая гибридная архитектура была предложена Р. Хехт-Нильсеном и имеет название сети встречного распространения [1-3,7,9]. Нейроны слоя Кохонена обучаются без учителя, на основе самоорганизации, а нейроны распознающих слоев адаптируются с учителем итерационными методами. Пример такой структуры для решения задачи классификации сейсмических сигналов приведен на рис. 4.5.
Второй уровень нейросети используется для кодирования информации. Весовые коэффициенты t
ij
(i =1,..., M; j=1,2) — коэффициенты от i-го нейрона слоя Кохонена к j-му нейрону выходного слоя рассчитываются следующим образом:
Выход нейронов второго слоя определяется выражением: (11)
R — пороговое значение (0 < R < 1) . Пороговое значение R можно выбрать таким образом, чтобы с одной стороны не были потеряны значения активированных кластеров, а с другой стороны — отсекался "шум не активизированных кластеров".
В результате на каждом шаге обработки исходных данных на выходе получаются значения S
j
, которые характеризуют явление, породившее данную входную ситуацию (
4.5 Выводы по разделу Итак, подводя итог данной главе, следует сказать, что это далеко не полный обзор нейросетевых архитектур, которые успешно справляются с задачами классификации. В частности ничего не было сказано о вероятностных нейронных сетях, о сетях с базисно радиальными функциями, о использовании генетических алгоритмов для настройки многослойных сетей и о других, пусть менее известных, но хорошо себя зарекомендовавших. Соответственно проблема выбора наиболее оптимальной архитектуры для решения задачи классификации сейсмических сигналов вполне актуальна. В идеале, конечно хотелось бы проверить эффективность хотя бы нескольких из них и выбрать наилучшую. Но для этого необходимо проводить более масштабные исследования, которые займут много времени. На данном этапе исследований была сделана попытка использовать хорошо изученные нейронные сети и алгоритмы обучения для того, чтобы убедиться в эффективности подхода в целом. В главе 6 детально обсуждается нейросеть, которая была исследована в рамках настоящей дипломной работы. 5. Методы предварительной обработки данных Если возникает необходимость использовать нейросетевые методы для решения конкретных задач, то первое с чем приходится сталкиваться — это подготовка данных. Как правило, при описании различных нейроархитектур, по умолчанию предполагают, что данные для обучения уже имеются и представлены в виде, доступном для нейросети. На практике же именно этап предобработки может стать наиболее трудоемким элементом нейросетевого анализа. Успех обучения нейросети также может решающим образом зависеть от того, в каком виде представлена информация для ее обучения. В этой главе рассматриваются различные процедуры нормировки и методы понижения размерности исходных данных, позволяющие увеличить информативность обучающей выборки. 5.1 Максимизация энтропии как цель предобработки Рассмотрим основной руководящий принцип, общий для всех этапов предобработки данных. Допустим, что в исходные данные представлены в числовой форме и после соответствующей нормировки все входные и выходные переменные отображаются в единичном кубе. Задача нейросетевого моделирования — найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для статистического моделирования являются примеры из обучающей выборки. Чем больше бит информации принесет пример — тем лучше используются имеющиеся в нашем распоряжении данные.
Рассмотрим произвольную компоненту нормированных (предобработанных) данных:
Общий принцип предобработки данных для обучения, таким образом состоит в максимизации энтропии входов и выходов.
5.2 Нормировка данных Как входами, так и выходами могут быть совершенно разнородные величины. Очевидно, что результаты нейросетевого моделирования не должны зависеть от единиц измерения этих величин. А именно, чтобы сеть трактовала их значения единообразно, все входные и выходные величин должны быть приведены к единому масштабу. Кроме того, для повышения скорости и качества обучения полезно провести дополнительную предобработку, выравнивающую распределения значений еще до этапа обучения. Индивидуальная нормировка данных
Приведение к единому масштабу обеспечивается нормировкой каждой переменной на диапазон разброса ее значений. В простейшем варианте это — линейное преобразование:
Линейная нормировка оптимальна, когда значения переменной
Линейное преобразование, представленное выше, не способно отнормировать основную массу данных и одновременно ограничить диапазон возможных значений этих данных. Естественный выход из этой ситуации — использовать для предобработки данных функцию активации тех же нейронов. Например, нелинейное преобразование
Все выше перечисленные методы нормировки направлены на то, чтобы максимизировать энтропию каждого входа (выхода) по отдельности. Но, вообще говоря, можно добиться гораздо большего, максимизируя их совместную энтропию. Существуют методы, позволяющие проводить нормировку для всей совокупности входов, описание некоторых из них приведено в [4]. 5.3 Понижение размерности входов Поскольку заранее неизвестно насколько полезны те или иные входные переменные для предсказания значений выходов, возникает соблазн увеличивать число входных параметров, в надежде на то, что сеть сама определит, какие из них наиболее значимы. Однако чаще всего это не приводит к ожидаемым результатам, а к тому же еще и увеличивает сложность обучения. Напротив, сжатие данных, уменьшение степени их избыточности, использующее существующие в них закономерности, может существенно облегчить последующую работу, выделяя действительно независимые признаки. Можно выделить два типа алгоритмов, предназначенных для понижения размерности данных с минимальной потерей информации:
Рассмотрим более подробно оба типа алгоритмов. 5.3.1 Отбор наиболее информативных признаков Для того, чтобы понять какие из входных переменных несут максимум информации, а какими можно пренебречь необходимо либо сравнить все признаки между собой и определить степень информативности каждого из них, либо пытаться найти определенные комбинации признаков, которые наиболее полно отражают основные характеристики исходных данных. В разделе 3.2 был описан алгоритм, позволяющий упорядочить все признаки по мере убывания их значимости. Однако накладываемые ограничения не позволяют применять его для более распространенных задач. Для выбора подходящей комбинации входных переменных используется так называемые генетические алгоритмы [5], которые хорошо приспособлены для задач такого типа, поскольку позволяют производить поиск среди большого числа комбинаций при наличии внутренних зависимостей в переменных. 5.3.2 Сжатие информации. Анализ главных компонент Самый распространенный метод понижения размерности — это анализ главных компонент (АГК) . Традиционная реализация этого метода представлена в теории линейной алгебры. Основная идея заключается в следующем: к данным применяется линейное преобразование, при котором направлениям новых координатных осей соответствуют направления наибольшего разброса исходных данных. Для этих целей определяются попарно ортогональные направления максимальной вариации исходных данных, после чего данные проектируются на пространство меньшей размерности, порожденное компонентами с наибольшей вариацией [4]. Один из недостатков классического метода главных компонент состоит в том, что это чисто линейный метод, и соответственно он может не учитывать некоторые важные характеристики структуры данных. В теории нейронных сетей разработаны более мощные алгоритмы, осуществляющие “нелинейный анализ главных компонент” [3]. Они представляют собой самостоятельную нейросетевую структуру, которую обучают выдавать в качестве выходов свои собственные входные данные, но при этом в ее промежуточном слое содержится меньше нейронов, чем во входном и выходном слоях. (рис 5.3) . Сети подобного рода носят название — автоассоциативные сети.
Чтобы восстановить свои входные данные, сеть должна научиться представлять их в более низкой размерности. Базовый алгоритм обучения в этом случае носит название
правило обучения Ойя
для однослойной сети. Учитывая то, что в такой структуре веса с одинаковыми индексами в обоих слоях одинаковы, дельта-правило обучения верхнего (а тем самым и нижнего) слоя можно записать в виде:
d — количество нейронов на входном ми выходном слоях (размерность вектора признаков) ; y i — выход с i -го нейрона внутреннего слоя, i=1, …, M M — количество нейронов на внутреннем слое;
w ij =w kj — веса сети, соответственно между входным — скрытым и скрытым — выходным слоями. Скрытый слой такой сети осуществляет оптимальное кодирование входных данных, и содержит максимально возможное при данных ограничениях количество информации. После обучения внешний интерфейс ( w ij ) (рис. 5.4) может быть сохранен и использован для понижения размерности.
Нелинейный анализ главных компонентов
Главное преимущество нейроалгоритмов в том, что они легко обобщаются на случай нелинейного сжатия информации, когда никаких явных решений уже не существует. Можно заменить линейные нейроны в описанных выше сетях — нелинейными. С минимальными видоизменениями нейроалгоритмы будут работать и в этом случае, всегда находя оптимальное сжатие информации при наложенных ограничениях. Например, простая замена линейной функции активации нейронов на сигмоидную в правиле обучения Ойя:
Таким образом, нейроалгоритмы представляют собой удобный инструмент нелинейного анализа, позволяющий относительно легко находить способы глубокого сжатия информации и выделения нетривиальных признаков. 5.4 Выводы по разделу Конечно, описанными выше методиками не исчерпывается все разнообразие подходов к ключевой для нейроанализа проблеме формирования пространства признаков. Например, существуют различные методики, расширяющие анализ главных компонент. Также, большего внимания заслуживают генетические алгоритмы. Необъятного не объять. Главное, чтобы за деталями не терялся основополагающий принцип предобработки данных: снижение существующей избыточности всеми возможными способами. Это повышает информативность примеров и, тем самым, качество нейропредсказаний. 6. Реализация нейросетевой модели и исследование ее технических характеристик Ранее было показано, какими средствами нейроинформатики можно пытаться решить задачу идентификации типа сейсмического источника, какие процедуры целесообразно применять при предварительной подготовке данных, был приведен небольшой обзор различных алгоритмов обучения известных нейроархитектур. В этой главе представлено решение задачи на базе двухслойного персептрона, так как именно он был выбран на начальном этапе исследований. Дано также описание алгоритма обучения и методов его оптимизации. 6.1 Структура нейронной сети Итак, для решения задачи идентификации типа сейсмического события предлагается использовать одну из самых универсальных нейроархитектур — многослойный персептрон, а точнее его двухслойную реализацию (рис. 6.1) . Как показали эксперименты, увеличение числа скрытых слоев не приводит к лучшим результатам, а лишь усложняет процесс обучения, поэтому и была выбрана именно реализация с одним скрытым слоем нейронов. На вход сети подается p- мерный вектор признаков {x i , i=1,2, …, p}. Для определенности будем рассматривать случай, когда p=9 , хотя исследования проводились и для p=5, p=18. Оптимальное количество нейронов на скрытом слое H подбиралось экспериментально для разных p. Соответственно при p = 9 достаточно брать H равным также 9 или немного больше. Для разбиения исходных данных на два класса на выходе сети достаточно одного нейрона. Между входным и скрытым слоями, а также между скрытым и выходным слоями использовалась полносвязная структура. С учетом этих дополнений опишем принятые на рисунке 7.1 обозначения: p — размерность исходных данных (количество признаков используемых для классификации) ; H — число нейронов на скрытом слое; x i — компонента входного вектора признаков, i = 1, …, p ; x 0 є 1 — постоянное воздействие используемое для работы нейронной сети; w ji — весовые коэффициенты между входным и скрытым слоями, i = 0,1, …, p, j = 1, …, H; v k — весовые коэффициенты между скрытым и выходным слоями , k = 0,1, …, H. z j — значение выхода j-го нейрона скрытого слоя; z 0 є 1, j = 1, …, H;
y
— значение выходного нейрона сети (выход сети)
f 1 (x) – функция активации нейронов скрытого слоя; f 2 (x) – функция активации нейрона выходного слоя. В качестве функции активации f 1 (x) для нейронов скрытого слоя и f 2 (x) для единственного нейрона на выходе сети предлагается использовать одну и ту же функцию, а именно сигмоидную функцию активации, для краткости будем обозначать ее как f(x) :
Вид такой функции представлен на рис. 6.2 Т. к. значения функции f(x) ограничены в диапазоне [0,1], результат сети y(x) может принимать любые действительные значения из этого же диапазона, в следствии чего логично интерпретировать выходы сети следующим образом: если y(x) > 0.5 , то вектор принадлежит к одному классу (взрывы) , в противном случае к другому (землетрясения) . 6.2 Исходные данные На вход нейронной сети предлагается подавать вектора признаков составленные из сейсмограмм. О том, какие признаки были использованы для этой задачи и как они получены, было рассказано ранее в разделе 3.1. Стоит отметить, что проблема формирования векторов признаков — это исключительно проблема сейсмологии. Поэтому для исследования эффективности применения нейронных сетей в качестве исходных данных были использованы уже готовые выборки векторов, которые содержали в себе примеры и землетрясений и взрывов. Размерность векторов признаков p=9, хотя, как было отмечено в предыдущем разделе, проводились эксперименты и с другим количеством признаков .
Для работы с нейросетью рекомендуется использовать исходные данные не в первоначальном виде, а после предварительной обработки при помощи процедуры индивидуальной нормировки по отдельному признаку, описанной в разделе 5.2. Это преобразование состоит в следующем:
y=Ln(x) и z=(1/7) (y 1/7 -1) , и уже из этих значений формируются обучающие вектора. Такие преобразования приводят к большей кластеризации точек в многомерном пространстве, однако диапазон изменения каждого из признаков не нормирован относительно интервала [-1,1], а выбранная нормировка позволяет без потери информации перенести все входные значения в нужный диапазон. 6.3 Определение критерия качества системы и функционала его оптимизации
Если через
k — номер обучающей пары в обучающей выборке, k=1,2, …, n 1 +n 2 n 1 — количество векторов первого класса; n 2 — число векторов второго класса.
В качестве функционала оптимизации будем использовать критерий минимума среднеквадратической функции ошибки:
6.4 Выбор начальных весовых коэффициентов Перед тем, как приступить к обучению нейронной сети, необходимо задать ее начальное состояние. От того насколько удачно будут выбраны начальные значения весовых коэффициентов зависит, как долго сеть за счет обучения и подстройки будет искать их оптимальное величины и найдет ли она их. Как правило, всем весам на этом этапе присваиваются случайные величины равномерно распределенные в диапазоне [-A, A], например [-1,1], или [-3,3]. Однако, как показали эксперименты, данное решение не является наилучшим и в качестве альтернативы предлагается использовать другие виды начальной инициализации, а именно:
Шаг 1. Задать 12 случайных чисел x 1 , x 2 , …, x 12 равномерно распределенных в диапазоне [0,1]. x i Н R[0,1].
Шаг 2. Для искомых параметров a и s величина
2. Можно производить начальную инициализацию весов в соответствии с методикой, предложенной Nguyen и Widrow [7]. Для этой методики используются следующие переменные
Вычисляется норма
Обе предложенные методики позволили на практике добиться лучших результатов, в сравнении со стандартным алгоритмом начальной инициализации весов. 6.5 Алгоритм обучения и методы его оптимизации Приступая к обучению выбранной нейросетевой модели, необходимо было решить, какой из известных типов алгоритмов, градиентный (обратное распространения ошибки) или стохастический (Больцмановское обучение) использовать. В силу ряда субъективных причин был выбран именно первый подход, который и представлен в этом разделе. Обучение нейронных сетей как минимизация функции ошибки
Когда функционал ошибки нейронной сети задан (раздел 6.3) , то главная задача обучения нейронных сетей сводится к его минимизации. Градиентное обучение — это итерационная процедура подбора весов, в которой каждый следующий шаг направлен в сторону антиградиента функции ошибки. Математически это можно выразить следующим образом:
Метод обратного распространения ошибки
Исторически наибольшую трудность на пути к эффективному правилу обучения многослойных персептронов вызвала процедура расчета градиента функции ошибки
Разберем этот метод на примере двухслойного персептрона с одним нейроном на выходе. (рис 6.1) Для этого воспользуемся введенными ранее обозначениями. Итак,
Несмотря на универсальность, этот метод в ряде случаев становится малоэффективным. Для того, чтобы избежать вырожденных случаев, а также увеличить скорость сходимости функционала ошибки, разработано много модификаций стандартного алгоритма, в частности две из которых и предлагается использовать. Многостраничное обучение С математической точки зрения обучение нейронных сетей (НС) — это многопараметрическая задача нелинейной оптимизации. В классическом методе обратного распространения ошибки (single-режим) обучение НС рассматривается как набор однокритериальных задач оптимизации. Критерий для каждой задачи — качество решения одного примера из обучающей выборки. На каждой итерации алгоритма обратного распространения параметры НС (синаптические веса и смещения) модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации. Из теории оптимизации следует, что при решении многокритериальных задач модификации параметров следует производить, используя сразу несколько критериев (примеров) , в идеале — все. Тем более нельзя ограничиваться одним примером при оценке производимых изменений значений параметров. Для учета нескольких критериев при модификации параметров используют агрегированные или интегральные критерии, которые могут быть, например, суммой, взвешенной суммой или квадратным корнем от суммы квадратов оценок решения отдельных примеров.
В частности, в настоящих исследованиях изменения весов проводилось после проверки всей обучающей выборки, при этом функция ошибки рассчитывалась в виде:
k — номер обучающей пары в обучающей выборке, k=1,2, …, n 1 +n 2 n 1 — количество векторов первого класса; n 2 — число векторов второго класса. Как показывают тестовые испытания, обучение при использовании пакетного режима, как правило сходится быстрее, чем обучение по отдельным примерам. Автоматическая коррекция шага обучения В качестве еще одного расширения традиционного алгоритма обучения предлагается использовать так называемый градиентный алгоритм с автоматическим определением длины шага h. Для его описания необходимо определить следующий набор параметров:
В начале обучения записываются на диск значения весов и смещений сети. Затем происходит заданное число итераций обучения с заданным шагом. Если после завершения этих итераций значение функции ошибки не возросло, то шаг обучения увеличивается на заданную величину, а текущие значения весов и смещений записываются на диск. Если на некоторой итерации произошло увеличение функции ошибки, то с диска считываются последние запомненные значения весов и смещений, а шаг обучения уменьшается на заданную величину. При использовании автономного градиентного алгоритма происходит автоматический подбор длины шага обучения в соответствии с характеристиками адаптивного рельефа, и его применение позволило заметно сократить время обучения сети без потери качества полученного результата. Эффект переобучения Одна из наиболее серьезных трудностей изложенного подхода обучения заключается в том, что таким образом минимизируется не та ошибка, которую на самом деле нужно минимизировать, а ошибка, которую можно ожидать от сети, когда ей будут подаваться совершенно новые наблюдения. Иначе говоря, хотелось бы, чтобы нейронная сеть обладала способностью обобщать результат на новые наблюдения. В действительности сеть обучается минимизировать ошибку на обучающем множестве, и в отсутствие идеального и бесконечно большого обучающего множества это совсем не то же самое, что минимизировать "настоящую" ошибку на поверхности ошибок в заранее неизвестной модели явления [5]. Иначе говоря, вместо того, чтобы обобщить известные примеры, сеть запомнила их. Этот эффект и называется переобучением. Соответственно возникает проблема — каким методом оценить ошибку обобщения? Поскольку эта ошибка определена для данных, которые не входят в обучающее множество, очевидным решением проблемы служит разделение всех имеющихся в нашем распоряжении данных на два множества: обучающее — на котором подбираются конкретные значения весов, и валидационного — на котором оцениваются предсказательные способности сети. На самом деле, должно быть еще и третье множество, которое вообще не влияет на обучение и используется лишь для оценки предсказательных возможностей уже обученной сети. Ошибки, полученные на обучающем, валидационном и тестовом множестве соответственно называются ошибка обучения, валидационная ошибка и тестовая ошибка . В нейроинформатике для борьбы с переобучением используются три основных подхода:
Самым простым является первый метод. Он предусматривает вычисление во время обучения не только ошибки обучения, но и ошибки валидации, используя ее в качестве контрольного параметра. В самом начале работы ошибка сети на обучающем и контрольном множестве будет одинаковой. По мере того, как сеть обучается, ошибка обучения, естественно, убывает, и, пока обучение уменьшает действительную функцию ошибок, ошибка на контрольном множестве также будет убывать. Если же контрольная ошибка перестала убывать или даже стала расти, это указывает на то, что сеть начала слишком близко аппроксимировать данные и обучение следует остановить. Рисунок 6.5 дает качественное представление об этой методике. Использование этой методики в работе с сейсмическими данными затруднено тем обстоятельством, что исходная выборка очень мала, а хотелось бы как можно больше данных использовать для обучения сети. В связи с этим было принято решение отказаться от формирования валидационного множества, а в качестве момента остановки алгоритма обучения использовать следующее условие: ошибка обучения достигает заданного минимального уровня, причем значение минимума устанавливается немного большим чем обычно. Для проверки этого условия проводились дополнительные эксперименты, показавшие что при определенном минимуме ошибки обучения достигался относительный минимум ошибки на тестовых данных. Два других подхода для контроля переобучения предусматривают постепенное изменение структуры сети. Только в одном случае происходит эффективное вымывание малых весов (weight elimination) , т.е. прореживание малозначительных связей, а во втором, напротив, поэтапное наращивание сложности сети. [3,4,5]. 6.6 Формирование обучающей выборки и оценка эффективности обученной нейросетевой модели Из исходных данных необходимо сформировать как минимум две выборки — обучающую и проверочную. Обучающая выборка нужна для алгоритма настройки весовых коэффициентов, а наличие проверочной, тестовой выборки нужно для оценки эффективности обученной нейронной сети. Как правило, используют следующую методику: из всей совокупности данных случайным образом выбирают около 90% векторов для обучения, а на оставшихся 10% тестируют сеть. Однако, в условиях малого количества примеров эта процедура становится неэффективной с точки зрения оценивания вероятности ошибки классификации. В разделе 4.4 был описан другой, наиболее точный метод расчета ошибки классификации. Это, так называемый, метод скользящего экзамена (синонимы: cross-validation, “plug-in” -метод) . [7,9]. В терминах нейронных сетей основную идею метода можно выразить так: выбирается один вектор из всей совокупности данных, а остальные используются для обучения НС. Далее, когда процесс обучения будет завершен, предъявляется этот выбранный вектор и проверяется правильно сеть распознала его или нет. После проверки выбранный вектор возвращается в исходную выборку. Затем выбирается другой вектор, на оставшихся сеть вновь обучается, и этот новый вектор тестируется. Так повторяется ровно n 1 +n 2 раз, где n 1 –количество векторов первого класса, а n 2 — второго.
По завершению алгоритма общая вероятность ошибки P подсчитывается следующим образом:
N= n 1 +n 2 — общее число примеров; E– число ошибочных векторов (сеть неправильно распознала предъявляемый пример) .
Недостатком этого метода являются большие вычислительные затраты, связанные с необходимость много раз проводить процедуру настройки весовых коэффициентов, а в следствии этого и большое количество времени, требуемое для вычисления величины
Однако в случае с малым количеством данных для определения эффективности обученной нейронной сети рекомендуется применять именно метод скользящего экзамена или некоторые его вариации. Стоит отметить, что эффективность статистических методов классификации сейсмических сигналов также проверяется методом скользящего экзамена. Таким образом, применяя его для тестирования нейросетевого подхода, можно корректно сравнить результаты экспериментов с возможностями стандартных методов. 7. Программная реализация. При выборе программного обеспечения для решения определенной задачи с помощью нейронных сетей возможны два подхода: использование готовых решений в виде коммерческих пакетов или реализация основных идей в виде собственной программы. Первый подход позволяет получить быстрое решение, не вдаваясь в детальное изучение работы алгоритма. Однако, хорошие пакеты, в которых имеются мощные средства для реализации различных парадигм нейронных сетей, обработки данных и детального анализа результатов, стоят больших денег. И это сильно ограничивает их применение. Еще одним недостатком является то, что несмотря на свою универсальность, коммерческие пакеты не реализовывают абсолютно все возможности моделирования и настройки нейронных сетей, и не все из них позволяют генерировать программный код, что весьма важно. Если же возникает необходимость построить нейросетевое решение, адаптированное под определенную задачу, и реализованное в виде отдельного программного модуля, то первый подход чаще всего неприемлем. Именно такие требования и были выдвинуты на начальном этапе исследований. Точнее, необходимо было разработать программу, предназначенную для классификации сейсмических данных при помощи нейросетевых технологий, а также работающую под операционной системой Unix (Linux и Sun Solaris SystemV 4.2) . В результате была разработана программа, реализующая основные идеи нейроинформатики, изложенные в разделе 6. Следует отметить, что базовый алгоритм программы был выполнен под системой Windows 95, а лишь затем оптимизирован под Unix по той причине, что предложенная операционная система используется в узких научных и корпоративных кругах, и доступ к ней несколько ограничен, а для отладки программы требуется много времени. Для большей совместимости версий под различные платформы использовались возможности языка программирования С. 7.1 Функциональные возможности программы. В программе “nvclass. с” — (нейро-классификатор векторов данных) реализована модель двухслойного персептрона, представленная в разделе 6. Эта программа предназначена для соотнесения тестируемого вектора признаков сейсмической информации к одному из двух классов. Входные данные представляют собой предысторию сейсмических явлений конкретного региона, а также тестируемый вектор признаков, соответствующий сейсмическому событию, не включенному в предысторию. Эти данные считываются из соответствующих файлов в виде набора векторов признаков заданной размерности. Автоматически, в зависимости от размерности входных векторов, определяется конфигурация нейронной сети т.е. по умолчанию для заданной размерности входных данных выбирается определенное (рекомендуемое по результатам предварительных экспериментов) число нейронов в входном и скрытом слоях, хотя при желании эти параметры легко меняются. В качестве правила обучения нейронной сети реализован алгоритм обратного распространения ошибки и некоторые методы его оптимизации. После завершения процесса обучения тестируемый вектор признаков подается на вход уже обученной сети и вычисляется результат, по которому сеть с определенной вероятностью соотносит входной вектор к одному из заданных классов. Для дополнительной настройки нейронной сети в программе реализован ряд процедур, описанных в разделе 6. Из них можно выделить следующие:
Последняя процедура (многократное обучение сети) предусмотрена для устранения возможных ошибок идентификации. Для нейронной сети заданное число раз (Cycle) генерируются матрицы начальных весовых коэффициентов и выполняется алгоритм обучения и идентификации тестового вектора. По полученным результатам обучения и тестирования выбирается вариант наибольшего повторения и итоговое решение принимается исходя из него. Для исключения неоднозначности это число выбирается положительным, целым, нечетным. В программе “nvclass” предусмотрены следующие режимы функционирования:
“Внешний” режим предназначен для классификации вновь поступивших сейсмических данных и может быть использовать в следующих случаях
“Внутренний” режим служит для оценки вероятности ошибки идентификации сети и включает два подрежима — проверки правильности идентификации одного из векторов набора предыстории и последовательной проверки всех заданных векторов (“cross-validation” ) . Режим работы программы устанавливается в файле настроек. После завершения работы основные результаты записываются в соответствующий файл отчета, который потом можно использовать для детального анализа. Пример файла приведен в приложении 4. 7.2 Общие сведения.
7.3 Описание входного файла с исходными данными. В качестве исходных данных используется отформатированный текстовый файл, в котором хранится информация о размерности векторов, их количестве и сами вектора данных. Файл должен иметь форму числовой матрицы. Каждая строка матрицы соответствует одному вектору признаков. Количество признаков должно совпадать с параметром NDATA . Количество столбцов равно количеству признаков плюс два. Первый столбец содержит порядковый номер вектора в общей совокупности данных (соответствует последовательности 1,2,3,..., NPATTERN ) , а в последнем столбце записаны значения указателя классификатора: 1- для вектора из первого класса, 0 — для вектора из второго класса. Все числовые параметры разделяются пробелами и записываются в кодах ASCII. Пример файла приведен в приложении 2. 7.4 Описание файла настроек. Параметры настройки программы содержаться во входном файле “nvclass. inp” . Пример файла приведен в приложении 3. Для настройки используются следующие переменные: TYPE - РЕЖИМ РАБОТЫ ПРОГРАММЫ TYPE=1_1 Это значение соответствует внешнему режиму функционирования программы без обучения нейронной сети, т.е. тестирование на заранее обученной нейронной сети. При этом надо задать следующие параметры:
TYPE=1_2 Это значение соответствует внешнему режиму функционирования программы с обучением нейронной сети и тестированием на ней заданного вектора. Необходимо задать следующие параметры:
TYPE=2_1 Данное значение соответствует внутреннему режиму с проверкой одного из векторов из представленной выборки. Для функционирования программы необходимо задать следующие параметры:
TYPE=2_2 При данном значении параметра программа будет функционировать во внутреннем режиме с последовательной проверкой всех векторов (“cross_validation” ) . Необходимо задать следующие параметры:
NDATA РАЗМЕРНОСТЬ ВЕКТОРОВ ПРИЗНАКОВ Задается размерность векторов признаков, или количество признаков в каждом векторе наблюдений. Этой величине должны соответствовать все входные данные в текущем сеансе работы программы. NPATTERN КОЛИЧЕСТВО ВЕКТОРОВ ПРИЗНАКОВ Этот числовой параметр характеризует объем обучающей выборки и соответствует количеству строк во входном файле PATTERNFILE . PATTERNFILE ИМЯ ФАЙЛА С НАБОРОМ ВЕКТОРОВ ПРИЗНАКОВ Имя файла, содержащего наборы векторов признаков предыстории сейсмических явлений региона с указателями классификатора. TESTVECTOR ИМЯ ФАЙЛА С ТЕСТИРУЕМЫМ ВЕКТОРОМ ПРИЗНАКОВ. Имя файла, содержащего вектор признаков, который необходимо идентифицировать. Файл должен иметь форму строки (числа разделяются пробелами) . Количество признаков должно соответствовать переменной NDATA . NETWORKFILE ИМЯ ФАЙЛА С МАТРИЦАМИ ВЕСОВ ПРЕДВАРИТЕЛЬНО ОБУЧЕННОЙ СЕТИ . В этом параметре задано имя файла, содержащего матрицы весов предварительно обученной нейронной сети с фиксированной размерностью входных данных. Файл формируется на предыдущих этапах работы программы. Необходимо учитывать количество признаков NDATA (явно указанных в имени файла, под которые проектировалась нейронная сеть (NDATA соответствует количеству входов сети) и символьную аббревиатуру региона, из которого получена сейсмическая информация. RESNETFNAME ИМЯ ВЫХОДНОГО ФАЙЛА С МАТРИЦАМИ ВЕСОВ ОБУЧЕННОЙ СЕТИ Имя файла, содержащего параметры спроектированной и обученной нейронной сети в данном сеансе эксплуатации программы. В имени файла обязательно следует указывать символьную абревиатуру региона, из которого получена сейсмическая информация и размерность векторов признаков NDATA обрабатываемой информации, чтобы избежать путаницы в интерпретации разных моделей. (Например, norv18. net или isrl9. net) . NUMBERVECTOR ПОРЯДКОВЫЙ НОМЕР ВЕКТОРА ПРИЗНАКОВ Этот параметр соответствует номеру вектора признаков (номеру строки в первом столбце матрицы) из файла PATTERNFILE . Этот вектор признаков с указателем классификатора в дальнейшем будет интерпретироваться как тестовый вектор. Он удаляется из всего набора, а оставшиеся NPATTERN-1 векторов будут использованы в качестве обучающей выборки. REPORTFNAME ИМЯ ФАЙЛА ОТЧЕТА Имя файла с результатами работы программы. InitWeigthFunc ФУНКЦИЯ ИНИЦИАЛИЗАЦИИ НАЧАЛЬНЫХ ВЕСОВЫХ КОЭФФИЦИЕНТОВ СЕТИ. InitWeigthFunc=Gauss Начальные матрицы весовых коэффициентов будут выбраны как нормально распределенные случайные величины с математическим ожиданием Alfa и среднеквадратическом отклонении Sigma (N[Alfa, Sigma]) . InitWeigthFunc=Random Начальные матрицы весовых коэффициентов будут выбраны как равномерно распределенные случайные величины в диапазоне [-Constant, Constant]. (Значение по умолчанию — InitWeigthFunc= RandomDistribution[-3,3], т.е. Constant=3) Constant ДИАПАЗОН РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН Смотри InitWeigthFunc … Sigma СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕН-НЫХ СЛУЧАЙНЫХ ВЕЛИЧИН Смотри InitWeigthFunc … Alfa МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН Смотри InitWeigthFunc … WidrowInit NGUYEN-WIDROW ИНИЦИАЛИЗАЦИЯ. Параметр позволяет сформировать начальные весовые коэффициенты по методике предложенной Nguyen и Widrow. Возможные варианты: “Yes” — провести соответствующую инициализацию. “No” - не использовать эту процедуру. (Значение по умолчанию — “No” ) Shuffle ПЕРЕМЕШИВАНИЕ ВЕКТОРОВ ПРИЗНАКОВ При значении параметра “Yes” — входные вектора будут предварительно перемешаны. При “No” — вектора будут подаваться на вход сети в той последовательности, в которой они расположены во входном файле ( PATTERNFILE) . ( Значение по умолчанию — “Yes” ) . Scaling ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ВЕКТОРОВ ПРИЗНАКОВ. Этот параметр служит для использования в рамках программы “nvclass” процедуры масштабирования входных данных. Эта процедура позволяет значительно ускорить процесс обучения нейронной сети, а также качественно улучшает результаты тестирования. Возможные значения параметра: “Yes” ,” No” . (Значение по умолчанию — “Yes” ) . LearnToleranse ТОЧНОСТЬ ОБУЧЕНИЯ. Параметр определяющий качество обучения нейронной сети. При достижении заданной точности ε для каждого вектора признаков из обучающей выборки настройка весовых коэффициентов сети заканчивается и сеть считается обученной. (Значение по умолчанию — 0.1) . Eta КОЭФФИЦИЕНТ ОБУЧЕНИЯ НЕЙРОННОЙ СЕТИ . Значение коэффициента задает скорость и качество обучения нейронной сети. Используется для алгоритма обратного распространения ошибки. (Значение по умолчанию–1.0) MaxLearnCycles МАКСИМАЛЬНОЕ КОЛИЧЕСТВО ИТЕРАЦИЙ ОБУЧЕНИЯ Параметр задает количество итераций после которых процесс обучения будет автоматически завершен. (Величина по умолчанию- 2000) Loop КОЛИЧЕСТВО ПОВТОРОВ ОБУЧЕНИЯ. Параметр задает величину полных циклов функционирования программы (целое нечетное число) . В каждом цикле формируются начальные матрицы весов производится обучение сети и осуществляется классификация тестового вектора. Результаты всех циклов обрабатываются, и формируется итоговое заключение. (Значение по умолчанию=1) . 7.5 Алгоритм работы программы. Алгоритм работы программы зависит от режима, в котором она функционирует. Однако, для всех из них можно выделить базовый набор операций:
Инициализация В этом разделе происходит считывание всех данных из соответствующих файлов (файл с примерами обучающей выборки, файл с конфигурацией обученной сети, файл с примерами для тестирования) . Затем, в зависимости от режима функционирования, либо происходит инициализация всех весовых коэффициентов сети заданным образом, либо сразу начинается проверка тестовых векторов на обученной заранее нейронной сети, конфигурация которой считана из файла. Настройка. Если выбранный режим предусматривает выполнение алгоритма обучения нейронной сети, то программа, после считывания исходных данных, и начальной инициализации весовых коэффициентов выполняет процедуру их настройки до тех пор, пока не выполнится одно из условий остановки. Либо значение ошибки обучения достигнет желаемого уровня и сеть будет считаться обученной, либо количество итераций обучения превысит предварительно заданное максимальное число. По мере выполнения алгоритма автоматически формируется полный отчет о состоянии сети. Проверка тестовых векторов. На этом этапе происходит тестирование заданных векторов. Причем возможны два варианта: тестируемый вектор может быть считан из файла, а также можно задать номер тестируемого вектора в выборке исходных данных и тогда он не будет использован во время обучения. Результаты проверки записываются в файл отчета. 7.6 Эксплуатация программного продукта. Перед тем, как приступить к эксплуатации программного продукта рекомендуется ознакомиться с форматом данных, в котором должны быть записаны исходная выборка векторов и с основными переменными файла настроек программы. Для корректной работы в дальнейшем желательно придерживаться определенной последовательности действий:
7.7 Результат работы программы. Для исследований возможностей разработанного программного обеспечения были проведены различные эксперименты, основная цель которых — подобрать значения параметров настройки программы, при которых итоговые результаты ее работы содержали наименьшее количество ошибок идентификации. Методика, по которой оценивалась ошибка классификации, основана на подходе “cross-validation” . Эксперименты проводились на данных, полученных из сейсмограмм, записанных в Норвежской сейсмологической сети. В исходной выборке насчитывалось 86 событий из разных классов, из них соответственно 50 — землетрясений и 36 — взрывов. Исследования проводились для разного числа признаков идентификации, а именно для 18 и 9 размерных векторов признаков. Первая серия экспериментов была проведена на 18 размерных векторах. Структура нейронной сети соответствовала <18,9,1>, где 18 — количество нейронов во входном слое, 9- число нейронов на первом скрытом слое, 1-размерность выхода сети. Увеличение нейронов на скрытом слое не приводило к улучшению результатов, а при уменьшении возникали дополнительные ошибки, в следствии чего такая структура предлагается в качестве оптимальной. Далее представлены описание параметров настройки программы во входных файлах и результаты тестирования. В качестве начальной конфигурации использовались следующие значения настраиваемых параметров в файле “nvclass. inp” : TYPE=2_2 NDATA=18 NPATTERN=86 PatternFile=norv18. pat NetStructure=[18,9,1] WidrowInit=No Shuffle=Yes Scaling=Yes Eta=0.7 MaxLearnCycles=1950 Loop=5 Результаты экспериментов отражают количество ошибок идентификации от различных параметров настройки программы. Для примера рассмотрим влияние процедуры начальной инициализации весовых коэффициентов и точности обучения на ошибку классификации. На рисунках 7.1 и 7.2 едставлены эти результаты. Отметим, что более стабильные результаты получаются в случае инициализации весов при помощи нормально распределенных величин. Можно добиться всего лишь 4-5 ошибок из 86, что соответствует ошибке идентификации равной 5-6 процентов. Для 9 размерных векторов признаков была использована следующая структура нейронной сети <9,5,1>, т.е. 5 нейронов на скрытом слое было достаточно для получения хороших результатов. В качестве примера приведем исследования аналогичные тем, которые описаны выше. (Рис. 7.3,7.4) . Последнюю диаграмму можно представить в виде.
Уже сейчас можно сделать вывод, что при использовании не всего набора признаков идентификации, а некоторой части признаков результаты заметно улучшаются. Причем для случая 9 –размерных признаков особую роль процедура начальной инициализации не играет. Представленные эксперименты не отражают полной картины о возможностях применения нейронных сетей для идентификации типа сейсмического события, но они экспериментально подтверждают эффективность нейросетевых технологий для решения этой задачи. 8. Заключение Проведенные исследования подтвердили эффективность применения нейросетевых технологий для идентификации типа источника сейсмических события. При определенных настройках нейронной сети можно добиться результатов, когда вероятность правильного распознавания составляет 96.5%. Ошибки возникают только на 3 векторах из 86. Если сравнивать полученные результаты с теми, которые можно достичь при использовании стандартных методов классификации, один из вариантов которых приведен в разделе 4, то они практически повторяют друг друга. И статистика и нейронные сети ошибаются одинаковое количество раз, причем на одних и тех же векторах. Из 86 событий статистические методы ошибаются на 3 векторах (1–землетрясение и 2-взрыва) , и нейросетевой классификатор также ошибается именно на этих векторах. Соответственно пока нельзя говорить о каком-то превосходстве одного метода над другим. Заметим, что в настоящих исследованиях были использованы довольно общие и универсальные технологии нейроинформатики (многослойные сети применяются для решения многих задач, но это не всегда самая оптимальная нейроструктура) , а применение более узких и специализированных нейронных парадигм в некоторых случаях позволяет получать лучшие результаты. В частности, при помощи нейропакетов на тех же данных были поставлены ряд экспериментов над сетями Кохонена, описанными в разделе 5.4. Результаты показали, что количество ошибок идентификации в большинстве случаев составляет 3-4 вектора, т.е. практически совпадают с результатами, полученными на многослойных сетях и классических методах. Итак, подводя итог всему выше сказанному, выделим основные результаты проведенных исследований:
В качестве дальнейших исследований, направленных на повышение эффективности нейросетевого решения, можно предложить следующие:
Список литературы.
Приложение. 1. Пример выборки сейсмограмм. В левом столбце представлены сейсмограммы, описывающие взрывы, а в правом — землетрясения.
Пример файла с векторами признаков. Представлена выборка из файла 9_Norv. txt, содержащего 9 размерные вектора признаков. NumOfPattern: 86 PatternDimens: 9 1 -14.3104 -13.2561 -13.4705 -13.4306 -14.1015 -13.3503 -13.3805 -13.7369 -0.3494 0 2 -14.6881 -13.6349 -12.9050 -13.4323 -14.2279 -13.4720 -13.2117 -13.5791 -1.2801 0 3 -14.4036 -14.1745 -13.8014 -12.7209 -14.6283 -13.9589 -13.4649 -12.9716 -0.8250 0 … 55 -14.3693 -13.4362 -11.4072 -12.3129 -14.8612 -13.3480 -12.8517 -13.4014 -0.7738 0 56 -14.2856 -12.6858 -13.8215 -13.4282 -14.0982 -13.1587 -13.2792 -13.7852 -1.3442 0 57 -14.4822 -13.1141 -13.7787 -13.4466 -13.6761 -13.2969 -13.6033 -13.9252 -0.6642 1 58 -13.5522 -13.1302 -13.5444 -14.1471 -13.2994 -13.2368 -13.9776 -14.4295 -0.9973 1 59 -14.8524 -11.9846 -13.7231 -14.2496 -13.4809 -13.0515 -13.8950 -14.3923 -1.8284 1 … 85 -14.5994 -13.6920 -12.8539 -13.7629 -14.1699 -13.2075 -13.3422 -13.6788 -11.9537 1 86 -14.3821 -13.6093 -12.8677 -13.7788 -14.1260 -13.3246 -13.2966 -13.6453 -11.4304 1 Файл с настройками программы # # Common parameters for programm "NVCLASS" # # # # # # # # # # # # # # # # # # # # # # 1_1 — OnlyTest mode, 1_2 — TestAfterLearn mode, # 2_1 — CheckOneVector, 2_2 — CrossValidation mode. # TYPE=2_2 NDATA=9 NPATTERN=86 PatternFile=9_Norv. txt NTEST=10 TestVector=vector. tst NetworkFile=9. net ResNetFname=9. net NumberVector=57 ReportFile=Report. txt Debug=Yes # # Next parameters was define in result experiments and if you will # change it, the any characteristics of Neural Net may be not optimal # (since may be better then optimal) . # # # # # # # # # # # # # 'NetStructure' must be: [NDATA, NUNIT1,1] (NOUT=1 always) # value 'AUTO'-'NetStructure' will be define the programm. (See help) . # example: [18,9,1], or [18,18,1], or [9,9,5,1] NetStructure=[18,12,1] # may be: [Gauss] or [Random] InitWeigthFunc=Gauss Constant=3 Alfa=0 Sigma=1.5 Widrow=No Shuffle=Yes Scaling=Yes LearnTolerance=0.1 Eta=1 MaxLearnCycles=50 Loop=3 #end of list Пример файла отчета. NVCLASS report — Wed Jun 02 15: 58: 02 1999 Type = 1_2 Neural Net — <18,12,1> PatternFile — vect. txt Test Vector(s) — vector. tst ResNetFname — 12. net LearnTolerance = 0.10 InitialWeigthFunc = Gauss[ 0.0,1.5] < Loop 1 > Learning cycle result: NumIter = 5 NumLE = 3 Error vector(s) : 58,59,63, +-----+------+--------+------+ | N | ID | Result |Target| +-----+------+--------+------+ | 1 | 24 | 0.1064 | 0 | | 2 | 25 | 0.9158 | 1 | | 3 | 26 | 0.0452 | 0 | | 4 | 27 | 0.0602 | 0 | | 5 | 28 | 0.0348 | 0 | | 6 | 29 | 0.0844 | 0 | | 7 | 30 | 0.1091 | 0 | | 8 | 31 | 0.0821 | 0 | | 9 | 32 | 0.0298 | 0 | | 10 | 33 | 0.2210 | 0 | +-----+------+--------+------+ < Loop 2 > Learning cycle result: NumIter = 5 NumLE = 5 Error vector(s) : 33,34,55,58,63, +-----+------+--------+------+ | N | ID | Result |Target| +-----+------+--------+------+ | 1 | 24 | 0.1279 | 0 | | 2 | 25 | 0.9929 | 1 | | 3 | 26 | 0.0960 | 0 | | 4 | 27 | 0.1463 | 0 | | 5 | 28 | 0.1238 | 0 | | 6 | 29 | 0.1320 | 0 | | 7 | 30 | 0.1478 | 0 | | 8 | 31 | 0.1235 | 0 | | 9 | 32 | 0.0740 | 0 | | 10 | 33 | 0.5140 | 1 | +-----+------+--------+------+ Файл описания функций, типов переменных и используемых библиотек “nvclass. h” ./* * --- Neuro classificator--* * Common defines */ #include <stdio. h> #include <ctype. h> #include <stdlib. h> #include <string. h> #include <stdarg. h> #include <time. h> #include <math. h> //#include <unistd. h> //#include <sys/file. h> #include <fcntl. h> #define DefName "nvclass. inp" #define MAXDEF 100 #define MAXLINE 256 #define NMAXPAT 100 #define NMXINP 20 #define NMXUNIT 20 #define CONT 0 #define EXIT_OK 1 #define EXIT_CNT 2 #define RESTART 911 #define MAXEXP 700 /* Max arg exp(arg) without error 'OVERFLOW' */ #define Random 10 #define Gauss 20 #define OK 0 #define Error 1 #define Yes 77 #define No 78 #define Min 0 /* Find_MinMax(...) */ #define Max 1 #define TYPE_ONE 21 #define TYPE_TWO 22 #define TYPE_THREE 23 #define TYPE_FOUR 24 int NDATA = 0; int NUNIT1 = 0; int NUNIT2 = 0; int NUNIT3 = 0; int NOUT = 1; int NPATTERN = 0; /* Number of input pattern*/ int NWORK = 0; /* Number of work pattern*/ int NTEST= 0; /* Number of test pattern*/ int result; int STOP = 0; int NumOut = 250; /* Number of itteration, after which show result in debugfile. */ int Num_Iter=10;/* The parameters requred in the procecc of */ float Percent=0.25; /* dinamic lerning with change 'eta' */ float LearnTolerance = 0.10; float TestTolerance = 0.5; float MAX_ERR=0.00001; /* min error */ float eta = 1.0; /* learning coefficient*/ float MIN_ETA=0.000001; float **Array_MinMax; int *Cur_Number; float W1[NMXINP][NMXUNIT]; float W2[NMXUNIT]; float PromW1[NMXINP][NMXUNIT]; float PromW2[NMXUNIT]; float PromW1_OLD[NMXINP][NMXUNIT]; float PromW2_OLD[NMXUNIT]; float Err1[NMXUNIT]; float Err2; float OLD_ERROR; float GL_Error=0.0; float Out1[NMXUNIT]; float Out2; char NetStr[20]="Auto"; /* String with pattern of Net Structure*/ int Type = TYPE_THREE; /* Enter the mode of work of programm */ int InitFunc = Random; /* Random [=10] weigth will RandomDistribution Gauss [=20] —... GaussianDistributon */ float Constant = 1; /* RandomDistribution [-Constant, Constant]*/ float Alfa = 0; /* GaussianDistribution [Alfa, Sigma]*/ float Sigma = 1; /*... */ int Widrow = No; /* Nguyen-Widrow initialization start weigth*/ int Loop = 1; /* Number repeat of Learning cycle */ char *PatternFile; /* File with input patterns*/ char *TestVector; char *ReportFile="report. txt"; /* name of report file */ char *NetworkFile; /* Name of input NetConfig file */ char *ResNetFname; /* Name of output NetConfig file */ int DEBUG = Yes; /* if 'Yes' then debug info in the DebugFile */ char *DebugFile="Logfile. log"; /* Name of the debug file*/ int NumberVector = 0; /* Number of TEST vector */ int Shuffle = Yes; /* Flag — shuffle the input vectors*/ int Scaling = Yes; /* Scaling input vector */ int MaxLearnCycles = 1999; /* Max number of learning iteration */ FILE *Dfp; /* Debug file pointer */ FILE *Rfp; /* Report file pointer*/ typedef struct Pattern { int ID; /* ID number this vector in all set of pattern */ float *A; /* pattern (vector) A={a[0], a[1],..., a[NDATA]} */ float Target; /* class which this vector is present*/ } PAT; PAT *Input; PAT *Work; PAT *Test; /* lines in defaults file are in the form "NAME=value" */ typedef struct Default { char *name; /* name of the default */ char *value; /* value of the default */ } DEF; /* structure of statistics info about one test vector */ typedef struct Statistic { int ID; /* Primery number from input file */ float Target; float TotalRes; /* Total propability */ int Flag; /* Flag = 1, if vector was error and = 0 in over case */ float *result; /* Result of testing vector on current iteration */ int *TmpFlag; /* analog 'Flag' on current itteration */ int *NumIter; /* Number iteration of learning on which Learning cycle STOPED */ int **NumLE; /* Error vectors after cycle of learning was test*/ } STAT; /* structure of the some result of learning cycle */ typedef struct ResLearning { int NumIter; int LearnError[NMAXPAT+1]; /* A[0]-count of error, A[1]-ID1, A[2]-ID2,... A[NMAXRL]-ID?. */ } RL; /* function prototypes */ void OnlyTestVector(void) ; void TestAfterLearn (void) ; void CheckOneVector (void) ; void CrossValidation (void) ; DEF **defbuild(char *filename) ; DEF *defread(FILE *fp) ; FILE *defopen (char *filename) ; char *defvalue(DEF **deflist, const char *name) ; int defclose(FILE *fp) ; void defdestroy(DEF **, int) ; void getvalues(void) ; void Debug (char *fmt,...) ; void Report (char *fmt,...) ; void Widrow_Init(void) ; int Init_W(void) ; float RavnRaspr(float A, float B) ; float NormRaspr(float B, float A) ; void ShufflePat(int *INP, int Koll_El) ; float F_Act(float x) ; float Forward (PAT src) ; int LearnFunc (void) ; int Reset (float ResErr, int Cnt, int N_Err) ; void Update_Last (int n, float Total_Out) ; void Update_Prom1 (int n) ; void Prom_to_W (void) ; void Update_All_W (int num, float err_cur) ; void Init_PromW(void) ; void Prom_to_OLD(void) ; int CheckVector(float Res, PAT src) ; int *TestLearn(int *src) ; RL FurtherLearning(int NumIteration, float StartLearnTolerans, float EndLearnTolerans, RL src) ; STAT *definestat (PAT src) ; STAT **DefineAllStat (PAT *src, int Num) ; void FillStatForm (STAT *st, int iteration, float res, RL lr) ; void FillSimpleStatForm (STAT *st, float res) ; void destroystat (STAT *st, int param) ; void DestroyAllStat (STAT **st, int Num) ; void PrintStatHeader(void) ; void printstat(STAT *st) ; void PrintStatLearn(RL src) ; void PrintTestStat(STAT **st, int len) ; void PrintErrorStat (STAT **st, int Len) ; int DefineNetStructure (char *ptr) ; void getStructure(char buf[20]) ; PAT patcpy (PAT dest, PAT src) ; PAT* LocPatMemory(int num) ; void ReadPattern (PAT *input, char *name, int Len) ; void FreePatMemory(PAT* src, int num) ; void ShowPattern (char *fname, PAT *src, int len) ; void ShowVector(char *fname, PAT src) ; float getPatTarget (float res) ; PAT* DataOrder (PAT* src, int Len, int Ubit, PAT* dest, PAT* test) ; void FindMinMax (PAT *src, int Dimens, int Num_elem, float **Out_Array) ; void ConvX_AB_01(PAT src) ; int *DefineCN (int len) ; int getPosition (int Num, int *src, int Len) ; void DestroyCN (int *src) ; void ShowCurN (int LEN) ; float **LocateMemAMM(void) ; void FreeAMM (float **src) ; void WriteHeaderNet(char *fname, float **src) ; void WriteNet (char *fname, int It) ; void ReadHeaderNet(char *fname, float **src) ; int ReadNet (char *fname, int It) ; FILE *OpenFile(char *name) ; int CloseFile(FILE *fp) ; /* End of common file */ Файл автоматической компиляции программы под Unix -“Makefile” . CC= cc LIBS= -lm OBJ= nvclass. o nvclass: $(OBJ) $(CC) -o nvclass $(LIBS) $(OBJ) nvclass. o: nvclass. c Основной модуль — “nvclass. с” /* * Neuron Classificator ver 1.0 */ #include "common. h" /* ========================= * MAIN MODULE * ========================= */ void main (int argc, char *argv[]) { int i; char buf[MAXLINE], PrName[20], *ptr; time_t tim; time(&tim) ; /* UNIX Module */ Dfp = OpenFile(DebugFile) ; strcpy(buf, argv[0]) ; ptr = strrchr(buf, '/') ; ptr++; strcpy(PrName, ptr) ; Debug ("\n\n'%s' — Started %s", PrName, ctime(&tim) ) ; getvalues() ; Rfp = OpenFile(ReportFile) ; DefineNetStructure(NetStr) ; /* NetStr string from input file */ getStructure(buf) ; Debug ("\nNeyral net %s", buf) ; Input = LocPatMemory(NPATTERN) ; Work = LocPatMemory(NPATTERN) ; Array_MinMax = LocateMemAMM() ; Cur_Number = DefineCN (NPATTERN) ; printf("\nMetka — 1") ; if (Type == TYPE_ONE) OnlyTestVector () ; if (Type == TYPE_TWO) TestAfterLearn () ; if (Type == TYPE_THREE) CheckOneVector () ; if (Type == TYPE_FOUR) CrossValidation() ; time(&tim) ; Debug ("\n\n%s — Normal Stoped %s", PrName, ctime(&tim) ) ; CloseFile(Dfp) ; CloseFile(Rfp) ; FreeAMM (Array_MinMax) ; DestroyCN (Cur_Number) ; FreePatMemory(Input, NPATTERN) ; FreePatMemory(Work, NPATTERN) ; } /* * ^OnlyTestVectors — read net from (NetworkFile) and test the TestVector(s) */ void OnlyTestVector(void) { char buf[MAXLINE+1]; STAT **st, *stat; int i, j; float Res; Debug ("\nOnlyTestVector proc start") ; Debug ("\n NPATTERN = %d", NPATTERN) ; Debug ("\n NTEST = %d", NTEST) ; Test = LocPatMemory(NTEST) ; ReadPattern(Test, TestVector, NTEST) ; /* ShowPattern ("1. tst", Test, NTEST) ;*/ PrintStatHeader() ; st = DefineAllStat (Test, NTEST) ; ReadHeaderNet(NetworkFile, Array_MinMax) ; if (Scaling == Yes) { for (i=0;i<NTEST;i++) ConvX_AB_01(Test[i]) ; } for (i=0; i < Loop ; i++) { Debug("\n----/ STEP = %d /-----", i+1) ; Report("\n < Loop %d > ", i+1) ; ReadNet(NetworkFile, i+1) ; for (j=0;j<NTEST;j++) { Res=Forward(Test[j]) ; CheckVector(Res, Test[j]) ; FillSimpleStatForm(st[j], Res) ; } PrintTestStat(st, NTEST) ; } DestroyAllStat (st, 1) ; FreePatMemory(Test, NTEST) ; } … /* --------------------------------* Debug to LOG_FILE and to CONSOLE */ /* debug for UNIX */ void Debug (char *fmt,...) { va_list argptr; int cnt=0; if ((Dfp! = NULL) && (DEBUG == Yes) ) { va_start(argptr, fmt) ; vfprintf(Dfp, fmt, argptr) ; fflush (Dfp) ; va_end(argptr) ; } } void Report (char *fmt,...) { va_list argptr; int cnt=0; if (Rfp! = NULL) { va_start(argptr, fmt) ; vprintf (fmt, argptr) ; vfprintf(Rfp, fmt, argptr) ; fflush (Rfp) ; va_end(argptr) ; } } /* debug for DOS */ /* void Debug (char *fmt,...) { FILE *file; va_list argptr; if (DEBUG == Yes) { if ((file = fopen(DebugFile, "a+") ) ==NULL) { fprintf(stderr, "\nCannot open DEBUG file. \n") ; exit(1) ; } va_start(argptr, fmt) ; vfprintf(file, fmt, argptr) ; va_end(argptr) ; fclose (file) ; } } void Report (char *fmt,...) { FILE *file; va_list argptr; if ((file = fopen(ReportFile, "a+") ) ==NULL) { fprintf(stderr, "Cannot open REPORT file. \n") ; exit(1) ; } va_start(argptr, fmt) ; vfprintf(file, fmt, argptr) ; vprintf(fmt, argptr) ; va_end(argptr) ; fclose (file) ; } */ /* * ^ReadPattern */ void ReadPattern (PAT *input, char *name, int Len) { int i=0, j=0, id, TmpNp=0, TmpNd=0, Flag=0; char *buf1="NumOfPattern: "; char *buf2="PatternDimens: "; char str[40], str1[10]; PAT Ptr; FILE *DataFile; float tmp; Debug ("\nReadPattern(%s, %d) — started", name, Len) ; Ptr. A =(float*) malloc (NDATA * sizeof(float) ) ; if ((DataFile = fopen(name, "r") ) == NULL) { Debug("\nCan't read the data file (%s) ", name) ; fclose(DataFile) ; exit (1) ; } if ((strcmp(name, TestVector) ) == 0) /* if read TestVector, then read */ Flag = 1; /* only ID and A[i]. (NO Target) */ fscanf(DataFile, "%s %s", str, str1) ; if ((strcmp(str, buf1) ) ==0) TmpNp = atoi (str1) ; Debug("\nNumOfPattern = %d", TmpNp) ; fscanf(DataFile, "%s %s", str, str1) ; if ((strcmp(str, buf2) ) ==0) TmpNd = atoi (str1) ; Debug("\nPatternDimens = %d", TmpNd) ; if (TmpNp! = Len) Debug ("\n\tWARNING! — NumOfPattern NOT EQUAL Param (%d! = %d) ", TmpNp, Len) ; if (TmpNd! = NDATA) Debug ("\n\tWARNING! — PatternDimens NOT EQUAL NDATA (%d! = %d) ", TmpNd, NDATA) ; for (i = 0; i < Len; i++) {fscanf(DataFile, "%d", &id) ; Ptr. ID = id; for (j=0; j < NDATA; j++) { fscanf (DataFile, "%f", &tmp) ; Ptr. A[j]=tmp; } if (Flag) tmp = -1; else fscanf(DataFile, "%f", &tmp) ; Ptr. Target = tmp; input[i]=patcpy(input[i], Ptr) ; } fclose(DataFile) ; } /* * ^LocPatMemory — locate memory for (PAT *) */ PAT* LocPatMemory(int num) { int i; PAT *src; src = (PAT *) malloc (num * sizeof(PAT) ) ; for (i=0; i< num; i++) {src[i]. ID = -1; src[i]. A = (float*) malloc (NDATA * sizeof(float) ) ; src[i]. Target = -1.0; } return (src) ; } void FreePatMemory(PAT* src, int num) { int i; for (i=0;i<num;i++) free (src[i]. A) ; free (src) ; } /* * Copies pattern src to dest. * Return dest. */ PAT patcpy (PAT dest, PAT src) { int i; dest. ID = src. ID; for (i=0;i<NDATA;i++) dest. A[i] = src. A[i]; dest. Target = src. Target; return dest; } ….. /* Random distribution value * rand() return x from [0,32767] -> x/32768 * -> x from [0,1] */ float RavnRaspr(float A, float B) {float x; x = (B-A) *rand() /(RAND_MAX+1.0) + A; return x; } float NormRaspr(float A, float B) { float mat_ogidanie=A, Sigma=B; float Sumx=0.0, x; int i; for (i=0;i<12;i++) Sumx = Sumx + RavnRaspr(0,1) ; /* from R[0,1] -> N[a, sigma]*/ x = Sigma*(Sumx-6) + mat_ogidanie; return x; } int Init_W (void) { int i, j; float A, B; time_t t, t1; t = time(NULL) ; t1=t; /* restart random generator*/ while (t==t1) srand((unsigned) time(&t) ) ; if (InitFunc == Random) { A = -Constant; B = Constant; Debug ("\nInit_W () --- Start (%ld) ) ", t) ; Debug ("\n InitFunc=Random[%4.2f, %4.2f]", A, B) ; for(i=0; i<=NDATA; i++) for(j=0; j<NUNIT1; j++) W1[i][j]=RavnRaspr(A, B) ; for(j=0; j <= NUNIT1; j++) W2[j]=RavnRaspr(A, B) ; } if (InitFunc == Gauss) { A = Alfa; B = Sigma; Debug ("\nInit_W () --- Start (%ld) ) ", t) ; Debug ("\n InitFunc=Gauss[%4.2f, %4.2f]", A, B) ; for(i=0; i<=NDATA; i++) for(j=0; j<NUNIT1; j++) W1[i][j] = NormRaspr(A, B) ; for(j=0; j <= NUNIT1; j++) W2[j] = NormRaspr(A, B) ; } if (Widrow == Yes) Widrow_Init() ; Debug ("\nInit_W — sucsefull ") ; return OK; } /* LearnFunc */ int LearnFunc (void) { int i, j, n, K, NumErr=0; int num=0; float err_cur=0.0, Res=0; time_t tim; float ep[NMAXPAT]; GL_Error=1.0; time(&tim) ; Debug ("\nLearnFunc () --- Started") ; Debug ("\n eta = %4.2f", eta) ; Debug ("\n LearnTolerance = %4.2f", LearnTolerance) ; Init_PromW() ; do { num++; err_cur = 0.0; NumErr = 0; for (n = 0; n < NWORK; n++) { K = Cur_Number[n]; Res=Forward(Work[K]) ; ep[n]=fabs(Res-Work[K]. Target) ; if (ep[n] > LearnTolerance) { NumErr++; Init_PromW() ; Update_Last(K, Res) ; Update_Prom1(K) ; Prom_to_W() ; } err_cur = err_cur + (ep[n]*ep[n]) ; } err_cur=0.5*(err_cur/NWORK) ; result = Reset(err_cur, num, NumErr) ; if ((num % NumOut) ==0) Debug("\nStep: %d NumErr: %d Error: %6.4f", num, NumErr, err_cur) ; } while (result == CONT || result == RESTART) ; Debug("\nStep: %d NumErr: %d Error: %6.4f", num, NumErr, err_cur) ; return num; } Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
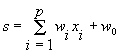 (1)
(1)
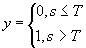 (3) В 1960 г. на основе таких нейронов Розенблатт построил первый в мире автомат для распознавания изображений букв, который был назван “перcептрон” (perception — восприятие) . Этот автомат имел очень простую однослойную структуру и мог решать только относительно простые (линейные) задачи. С тех пор были изучены и более сложные системы из нейронов, использующие в качестве передаточных сложные непрерывные функции. Одна из наиболее часто используемых передаточных функций называется сигмоидной (или логистической) (рис. 2б) и задается формулой
(3) В 1960 г. на основе таких нейронов Розенблатт построил первый в мире автомат для распознавания изображений букв, который был назван “перcептрон” (perception — восприятие) . Этот автомат имел очень простую однослойную структуру и мог решать только относительно простые (линейные) задачи. С тех пор были изучены и более сложные системы из нейронов, использующие в качестве передаточных сложные непрерывные функции. Одна из наиболее часто используемых передаточных функций называется сигмоидной (или логистической) (рис. 2б) и задается формулой
 (4)
(4)
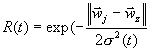 Шаг 6. Обновить размер окрестности s (t) и скорость h (t) s (t) =s (0) (1-t/t
max
) h (t) =h (0) (1-t/t
max
) Шаг 7. Если (t < t
max
) , то Шаг 2, иначе СТОП.
Шаг 6. Обновить размер окрестности s (t) и скорость h (t) s (t) =s (0) (1-t/t
max
) h (t) =h (0) (1-t/t
max
) Шаг 7. Если (t < t
max
) , то Шаг 2, иначе СТОП.
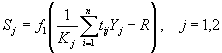 где:
где:
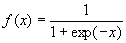 , с производной в виде
, с производной в виде
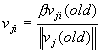 Смещения
Смещения
 В начало
В начало